hodoring

R 내부데이터, 공공데이터 등 여러 데이터들을 분석해보니 여러가지 함수들을 사용하게 되었습니다. 분석에 사용했던 함수들을 모수/비모수 혹은 범주형/연속형 에 따라 분류하여, 데이터에 따라 적당한 방법을 사용할 수 있는 방법을 작성하겠습니다.

Y : 연속형  ~  X : 범주형 (2그룹)

모수 : T - test [ 두 집단의 평균값 차이 ]

data = PlantGrowth
shapiro.test(data$weight)
data$gp = ifelse(data$group == "ctrl",1,0)
var.test(weight~gp, data)
t.test(weight~gp,data,var.equal=T)

- var.test 결과 : p-value > 0.05 이므로, 분산이 같다.

- t.test 결과 : p-value > 0.05 이므로, 두 그룹의 평균 차이는 통계적으로 유의미하지 않다.

비모수 : wilcox - test [ 두 집단의 중심 차이 : 순위 기반 비교]

wilcox.test(wt~sex, data)
aggregate(wt~sex,data,summary)

- wilcox.test 결과 : p-value < 0.05 이므로, 두 값의 중앙값 차이가 통계적으로 유의미하다.

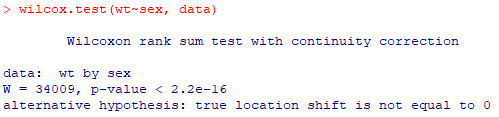
- mean-range table : 얼마나 차이나는지 보인다.

Y : 연속형  ~  X : 범주형 (3그룹)

모수 : ANOVA test [ 세 집단 이상의 평균값 차이 ]

data = PlantGrowth
by(data$weight, data$group, shapiro.test)
bartlett.test(weight~group, data)
ret = aov(weight~group, data)
summary(ret)
TukeyHSD(ret)

- shapiro.test 결과 : 정규성을 만족여부

- bartlett.test 결과 : p-value > 0.05 이므로, 그룹간 분산이 동일하다.

- aov 결과 : p-value < 0.05 이므로, 그룹간 평균차이가 통계적으로 유의미하다.

- TukeyHSD 결과 : diff - 두 그룹의 평균 차이, plot결과 0을 포함하면 그룹간 평균차이가 통계적으로 유의미하지 않음

비모수 : Kruskal [ 세 집단 이상의 중앙값 차이 ]

data = mtcars
data$cyl = as.factor(data$cyl)
by(data$mpg, data$cyl, shapiro.test)
ret = kruskal.test(mpg~cyl, data)
ret = pairwise.wilcox.test(data$mpg, data$cyl, p.adjust.method="bonferroni", exact=FALSE)
ret
 boxplot(mpg ~ cyl, data = mtcars,
+         main = "Miles per Gallon by Cylinder",
+         xlab = "Number of Cylinders",
+         ylab = "Miles per Gallon",
+         col = c("lightblue", "pink", "lightgreen"))
>         col = c("lightblue", "pink", "lightgreen"))

- shapiro.test 결과 : 모두 p-value > 0.05 이므로, 정규분포한다. 그러나, 데이터 수가 적으므로 해당 테스트를 진행한다.

- kruskal.test 결과 : p-value < 0.05 이므로, 그룹 간 중앙값 차이가 통계적으로 유의미하다.

- pairwise.wilcox.test 결과 : 사후검정 결과, 모두 p-value < 0.05 이므로, 중앙값 차이가 유의미하다. plot을 통해 확인한다.

Y : 연속형  ~  X : 연속형

정규분포 가정 : Pearson 상관분석 [ 두 연속형 변수 간의 선형 상관관계 측정 ]

- 두 변수 간의 관계가 선형적이어야함

data = cars
shapiro.test(data$speed)
shapiro.test(data$dist)
cor.test(data$speed, data$dist, method="pearson")
plot(data)
lines(lowess(data))

// 선형회귀
ret = lm(dist~speed, data)
summary(ret)
abline(ret)

- shapiro.test 결과 : 모두 p-value > 0.05 이면 pearson 정상적으로 사용, 해당 데이터에선 정규분포라 가정.

- cor.test 결과 : p-value < 0.05 이므로, 상관관계가 통계적으로 유의미. r > 0 이므로 강력한 양의 상관관계 가짐 

- plot -> lines : 경향선을 볼 수 있음

- lm 결과 : R-squared = 0.6511 이므로, speed가 dist의 약 65%를 설명한다.

 > Residuals : 잔차는 0에 가까울 수록 모델의 예측력이 좋음을 의미함

 > Coefficients : Estimate ( 변수가 1 오를 때, y가 얼마나 오르는가 ), Pr ( < 0.05 이면 통계적으로 유의하다 )

 > Multiple R-squared : 독립변수가 종속변수의 변동을 얼마나 설명하는가

 > F-statistic : p-value < 0.05 이면 모델 전체가 통계적으로 유의미하다.

 - plot -> abline : 추세선

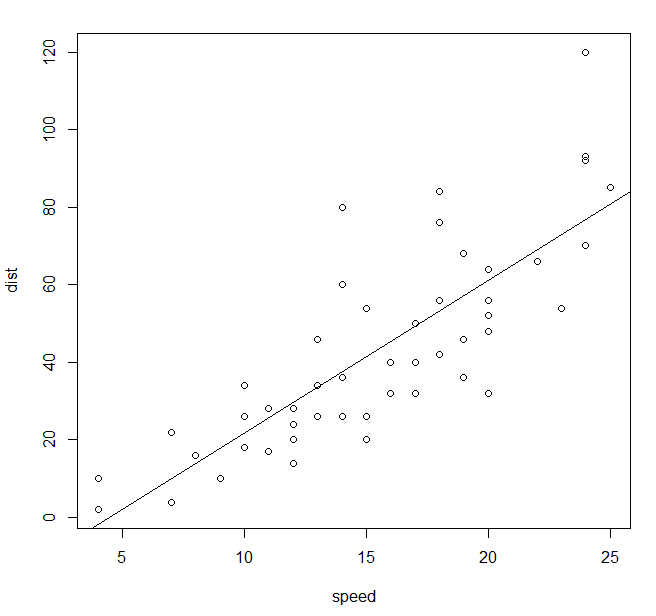
가정 요구하지 않음 : Spearman 상관분석 [ 두 변수의 비선형 관계 또는 순위 기반 관계 측정  ]

- 데이터를 순위로 변환한 후 상관계수 계산

data = iris
shapiro.test(data$Sepal.Length)
shapiro.test(data$Petal.Length)
cor.test(data$Sepal.Length, data$Petal.Length, method="spearman", exact=FALSE)
plot(data$Sepal.Length, data$Petal.Length)
lines(lowess(data$Sepal.Length, data$Petal.Length))

// 선형회귀
ret = glm(Petal.Length ~ Sepal.Length, data, family="gaussian")
summary(ret)
plot(data$Sepal.Length, data$Petal.Length)
abline(ret)

- shapiro.test 결과 : 정규분포 여부

- cor.test 결과 : spearman test 결과

 > p-value < 0.05 이므로, 두 변수간 관계가 통계적으로 유의미함

 > rho = 0.881.. 이므로, 두 변수는 강한 양의 단조 관계임

- plot : 비선형 경향성 보임

- glm : 선형회귀

 > Coefficients : Estimate ( 꽃바침 길이 1 증가시 꽃잎 길이 1.85 증가 ), Pr ( < 0.05 이므로, 통계적으로 유의미한 영향 )

 > AIS : 값이 작을수록 모델이 데이터를 더 잘 설명함

- plot > abline : 추세선

Y : 범주형  ~  X : 범주형

Crosstable + Chisq.test

data = mtcars
CrossTable(data$vs, data$gear)
chisq.test(data$vs, data$gear)
ret = glm(vs~gear, data, family=binomial)
summary(ret)
round(exp(cbind(coef(ret), confint(ret))), 3)

- CrossTable 결과 : 변수간 분포를 시각적으로 확인함

 > vs = 1 일때, 4단 기어의 비율이 높다 등.. 해석 가능

- chisq.test 결과 : p-value < 0.05 이므로, vs와 gear는 독립적이지 않음 ( 통계적으로 유의미한 관계가 있음 )

- glm 결과 : 로지스틱 회귀

 >  Coefficient :

     Estimate ( 기어 수 1증가할때 로그 오즈의 변화량 )

     Std.Error ( 표준오차. 작은수록 신뢰도 놓음 )

     z value ( z값 클수록 종속변수에 더 강한 영향 미침 )

     Pr ( p-value > 0.05 이므로, 통계적으로 유의하지 않음 )

- exp 결과 : odds 값 얻기

 > 기어수 1 증가하면 직렬엔진일 오즈가 1.788배 증가함. ( 기어수 증가할 수록 직렬엔진일 확률이 증가함 )

 > 신뢰수준 1을 포함하므로, gear의 효과는 통계적으로 유의미하지 않음

적절한 모델 찾기

data = mtcars
ret = glm(vs ~ wt + hp + factor(gear) + drat, data, family = binomial)
vif(ret)
step(ret)
ret2 = glm(formula = vs ~ hp, family = binomial, data = data)
lrtest(ret,ret2)
summary(ret2)

- vif 결과 : 다중공선성 확인 ( 10보다 크면 서로 영향을 많이 주므로, 없애야함 )

- step 결과 : 자동으로 AIC 가장 낮은 모델을 골라줌

- lrtest 결과 : p-value > 0.05 이므로, 두 모델 간 성능 차이가 유의미하지 않다. 즉 새로운 모델을 채택한다.

- summary 결과 : 최종 모델 확인

이번 게시글에선 주어진 txt파일을 분석해보겠습니다.

3개의 txt파일에 대한 정보입니다.

## ex1.txt  
# 대상자 번호  pid 
# 당뇨측정시점  redcap_event_name  
# 당화혈색소  HbA1c 
# HbA1c(당화혈색소) ≥ 6.5% : 당뇨 정의 

## ex2.txt  
# 체중_대상자 번호 BW_myhealth_id 
# 체중_측정 일시 BW_date_measured 
# 체중_측정값 BW_value 

## ex3.txt  
# 대상자 번호 pid 
# 대상자 나이 age  
# 대상자 성별 sex

1. 데이터 불러오기

input1 = read.table("exam302_1.txt", header=T, sep="\t")
input2 = read.table("exam302_2.txt", header=T, sep="\t")
input3 = read.table("exam302_3.txt", header=T, sep="\t")

3개의 파일을 각각 다른 변수에 할당합니다.

2. 데이터 전처리

input1 = input1[,c("pid","hba1c")]
input2 = input2[,c("pid","BW_value")]
input3 = input3[,c("pid","age")]

분석에 필요한 변수만 추출합니다.

data = merge(input3,input1,by="pid")
data = merge(data,input2,by="pid")

대상자번호(pid) 기준으로 하나의 테이블로 합칩니다.

data = data[data$"BW_value"<300 & data$"BW_value">0,]

체중이 비정상정으로 크거나 0인 행을 제거합니다.

data = na.omit(data)

결측값을 제거합니다.

mainData = data[!duplicated(data$pid),]
mainData = aggregate(cbind(BW_value, hba1c) ~ pid+age, data, mean)

pid 기준, 중복되는 행들이 많습니다. 체중과 당화혈색소를 평균내서 중복을 제거합니다.

가설 1 : 당뇨인 군과 당뇨가 아닌 군의 평균체중은 차이가 있다.

1. 데이터 불러오기

ret1 = mainData
ret1$"hba1c" = ifelse(ret1$"hba1c">=6.5,1,0)

가설1의 결과를 담을 변수 ret1에 전처리된 데이터를 저장합니다.

또한, 당뇨여부를 판단해야하므로 hba1c 열을 당뇨여부를 표시하도록 변경합니다.

2. 정규분포성 검사

qqnorm(ret1$BW_value[ret1$BW_value=="0"])
qqnorm(ret1$BW_value[ret1$BW_value=="1"])

..

샘플이 5000개보다 많으므로, 정규분포를 가정합니다.

3. 분산 비교

var.test(BW_value~hba1c,ret1)

var.test 결과 p-value > 0.05 이므로, 분산이 같다는 결과를 얻습니다.

4. 평균 비교

t.test(BW_value~hba1c,ret1,var.equal=T)

t.test 결과 p-value > 0.05 이므로, 평균이 같다는 결과를 얻습니다.

5. 함의

당뇨 여부와 평균체중은 통계적으로 유의한 차이가 없다.

두 집단의 평균체중 차이는 약 0.2 정도이다.

가설 2 : 당뇨환자의 연령그룹이 (,40) [40,60) [60,) 라면, 그룹별 평균체중은 차이가 있다.

1.  데이터 불러오기

ret2 = mainData[mainData$"hba1c">=6.5,]

가설2의 결과를 담을 변수 ret2에 전처리된 데이터를 저장합니다.

2.  정규분포성 검사

샘플이 5000개보다 많으므로, 정규분포를 가정합니다.

3. 등분산 검사

bartlett.test(BW_value~factor(gp),ret2)

bartlett.test 결과 p-value < 0.05 이므로, 분산이 다르다는 결과를 얻었습니다.

4. 평균 비교

oneway.test(BW_value~factor(gp), ret2, var.equal=F)

oneway.test 결과 p-value < 0.05 이므로 평균이 다르다는 결과를 얻었습니다.

5. 사후검정

pairwise.t.test(ret2$BW_value, ret2$gp, p.adjust.method="bonferroni")

해당 테스트 결과, 2,3 그룹에서 통계적으로 유의한 차이가 보였습니다.

만약 등분산이었다면..

result = aov(BW_value ~ gp, ret2)
plot(TukeyHSD(result))

그래프에서, 0을 포함하지 않는다면 통계적으로 유의한 차이를 보인 것이다.

질병관리청에서 제공하는 공공데이터를 R을 활용하여 분석해보겠습니다.

초기설정

질병관리청 > 국민건강영양조사 > 원시자료 > 다운로드 : 소스파일 다운로드
질병관리청 > 국민건강영양조사 > 원시자료 > 자료분석지침 : 이용지침서 다운로드

해당 사이트에서 얻은 소스파일(.sas) 을 분석하겠습니다.

이용지침서의 변수 설명을 보며 분석해야하니 해당 파일도 필요합니다.

(소스파일은 C:/workspace 에 위치합니다)

데이터 불러오기 및 다듬기

1. sas 파일을 불러오기 위한 외부 라이브러리를 설치합니다

install.packages("haven")
library("haven")

2. 작업디렉토리를 소스파일이 있는 장소로 설정합니다.

setwd("C:/workspace")

3. 데이터를 불러온 후 원하는 부분만 추출합니다

input = read_sas("sample.sas7bdat")
data = input[,c("age","sex","EC1_1","BP16_1","BP1","HE_BMI")]

이용지침서에 따르면, 

age : 나이

sex : 성별

EC1_1 : 경제활동상태

BP16_1 : 하루 평균 수면시간

BP1 : 스트레스

HE_BMI : bmi 지수

4. 사용하지 않는 데이터 제거

data = data[data$"BP16_1"<=24 & data$"EC1_1"<=2 & data$"BP1"<=4 & data$"HE_BMI">0,]

데이터 중 "응답없음"처럼 분석과 상관 없는 값을 제거합니다.

BP16_1 : 수면시간 >= 24

EC1_1 : 경제활동은 1,2가 유의미합니다

BP1 : 스트레스는 1,2,3,4가 유의미합니다

HE_BMI : BMI > 0

5. 결측치 제거

data = na.omit(data)

결측치(NA)를 제거합니다

경제활동 유무와 수면시간의 평균에 대한 비교

남성에 대한 결과값

1. 데이터 추출

retM = data[data$"age">29 & data$"age" < 61,]
retM = retM[retM$"sex"==1,]

30 ~ 60세의 남성에 대한 데이터를 retM 이라는 변수에 저장하겠습니다.

2. 정규분포성 검사

shapiro.test(retM$EC1_1)
shapiro.test(retM$BP16_1)

비교할 두 열의 정규분포성을 검사합니다.

두 결과 모두 p-value < 0.05 이므로, 정규분포하지 않다는 결과를 얻었습니다.

그러나, 표본이 충분히 많기 때문에 정규분포한다고 가정하고 분석을 이어가겠습니다.

3. 경제활동 여부에 따른 수면시간 비교

var.test(BP16_1~factor(EC1_1),data=retM)

var.test 결과 p-value < 0.05 이므로, 분산 값이 다르다는 결과를 얻었습니다.

t.test(BP16_1~factor(EC1_1), data=retM, var.equal=F)

t.test 결과 p-value < 0.05 이므로, 평균이 다르다는 결과를 얻었습니다.

4. 결과 분석

남성의 경우, 경제활동 여부에 따라 수면시간이 통계적으로 유의하게 차이가 있습니다.

여성에 대한 결과값

1. 데이터 추출 

retFM = data[data$"age">29 & data$"age" < 61,]
retFM = retM[retFM$"sex"==2,]

30 ~ 60세의 여성에 대한 데이터를 retFM 이라는 변수에 저장하겠습니다.

2. 정규분포성 검사

shapiro.test(retFM$EC1_1)
shapiro.test(retFM$BP16_1)

두 결과 모두 p-value < 0.05 이므로, 정규분포하지 않다는 결과를 얻었습니다.

남섬의 경우처럼, 표본이 충분히 많기 때문에 정규분포한다고 가정하고 분석을 이어가겠습니다.

3. 경제활동에 따른 수면시간 비교

var.test(BP16_1~factor(EC1_1),data=retFM)

var.test 결과 p-value < 0.05 이므로, 분산 값이 다르다는 결과를 얻었습니다.

t.test(BP16_1~factor(EC1_1), data=retFM, var.equal=F)

t.test 결과 p-value < 0.05 이므로, 평균이 다르다는 결과를 얻었습니다.

4. 결과 분석

여성의 경우도, 경제활동 여부에 따라 수면시간이 통계적으로 유의하게 차이가 있습니다.

최종 함의

남성과 여성의 경우 모두 경제활동 여부에 따른 수면시간이 통계적으로 유의하게 차이가 있다는 결론을 얻었습니다.

남성과 여성 모두 경제활동을 하지 않는 경우, 통계적으로 유의하게 수면시간이 길었습니다.

또한, 남성의 경우가 여성인 경우보다 경제활동 유무에 따른 수면시간 차이가 더 컸습니다.